The Fermi temperature
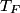 is defined as the Fermi energy is defined as the Fermi energy 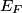 divided by the Boltzmann constant divided by the Boltzmann constant 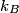 . The average speed of a conduction electron corresponds to a kinetic energy equal to the Fermi energy. That is . The average speed of a conduction electron corresponds to a kinetic energy equal to the Fermi energy. That is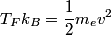 We solve this for  to obtain to obtain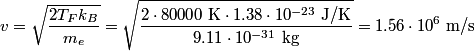 Therefore, answer (E) is correct. |